Introduction to Machine Learning 2023#
Last update June, 13 2023
%%file requirements.txt
matplotlib
pandas
numpy
scikit-learn
tensorflow
torch
jax
jaxlib
flax
astropy
plotly
%matplotlib inline
import pandas as pd
import numpy as np
import pylab as plt
from IPython.display import Markdown, display
In astronomy, the data rarely look like the shiny, eye-candy images that we see in press releases for example. Instead, our data often come as messy series of tables and images. It is the purpose of science to find the meaning of these data and turn them into a more useful formats.
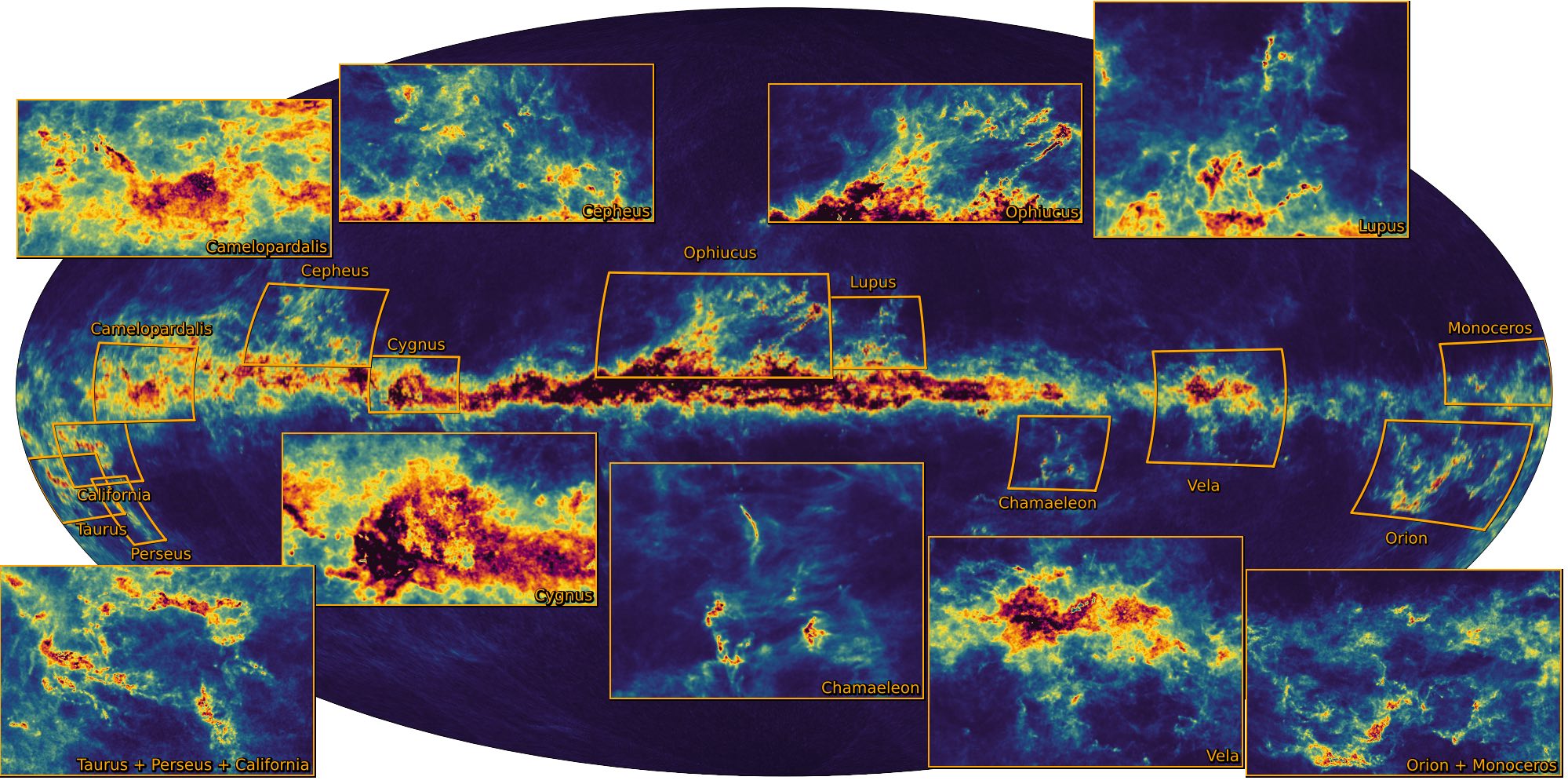
Fig. 7 Sky map from GSPPhot extinction from Gaia’s data release 3 Image credits: ESA/Gaia/DPAC.#
What is machine learning?#
In its essence, Machine learning refers to the ability of computer systems to automatically learn and improve from experience without explicit programming. We attribute the foundation of machine learning to Arthur Samuel (see image) who tought a computer how to play checkers in 1959 and to Tom Mitchell who gave it the modern spin in 1997: Machine Learning is the study of computer algorithm that allow computer programs to automatically improve through experience.

Fig. 8 “Field of study that gives computers the ability to learn without being explicitly programmed.” Arthur Samuel, Teaching a computer to play checkers, 1959 Left is the original black and white image. Right the image processed to infer colors using ML algorithm (colorize-it.com).#
Machine learning is part of the grand scheme of automated machine decisions. In computer science, a rule-based system is a system that stores and manipulate knowledge to interpret information or take decisions in a useful way. Normally, the term rule-based system only applies to systems involving human-crafted or curated rule sets. For instance in a factory, if an item is not conforming to the size or shape rule, it will be discarded.
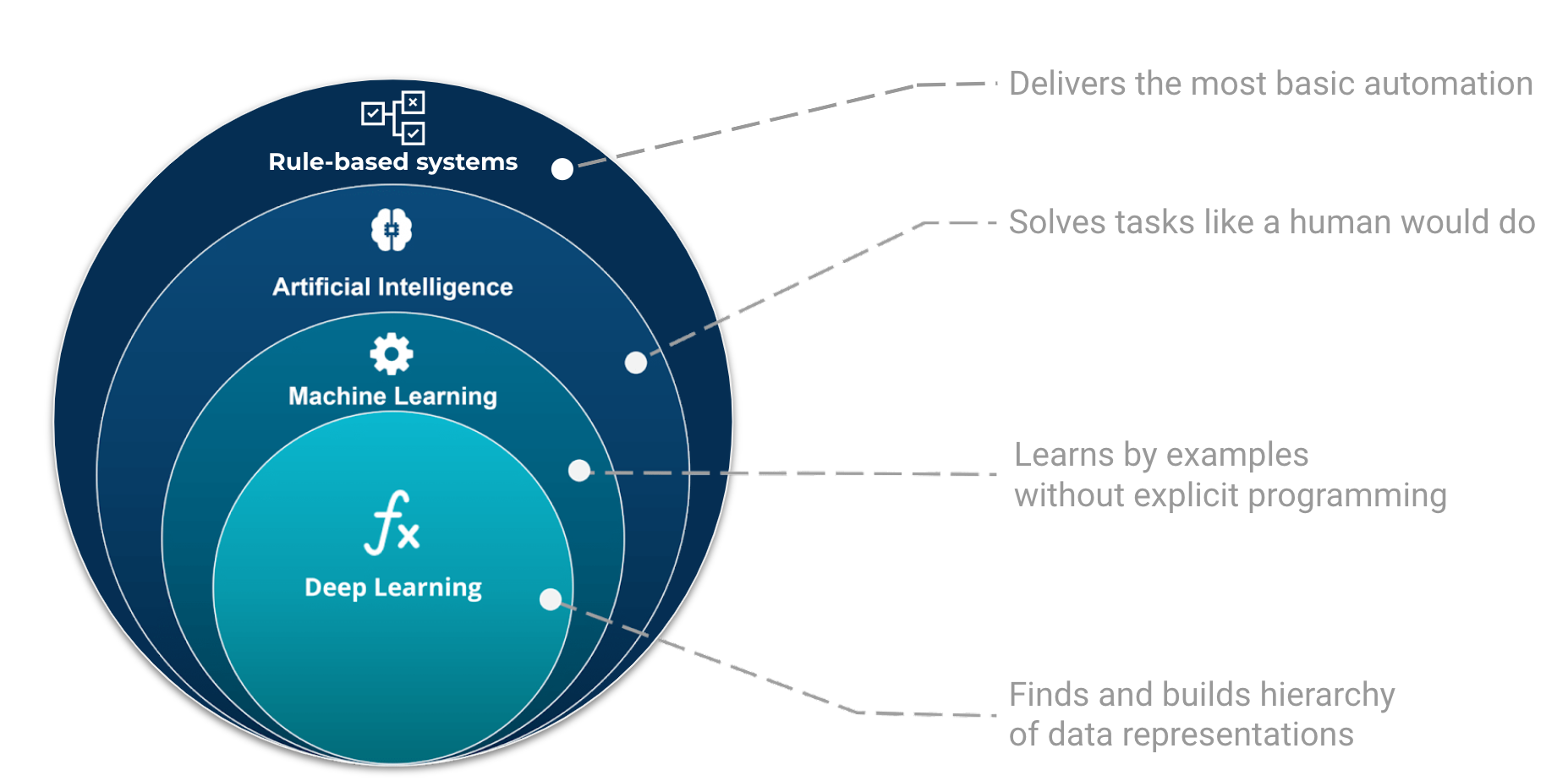
Fig. 9 The place and role of AI, ML, and Deep Learning in automated machine decisions. Image adapted from Tukijaaliwa, CC BY-SA 4.0, via Wikimedia Commons, original source#
If those sets of rules are not explicitly programmed but learned, we enter the domain of artificial intelligence, e.g. automatic rule inference. Artificial intelligence is broad and aims at tackling problems the way humans do. For example, evolutionary algorithms are a family of optimization algorithms inspired by processes of natural evolution. They help to solve complex optimization problems by iteratively improving a population of candidate solutions over multiple generations. The following shows the example of differential evolution optimization.
Show code cell source
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LogNorm
import numpy as np
from IPython.display import HTML
# Define the function to be optimized
def sphere(x):
return sum([xi**2 for xi in x])
# Define the function to be optimized (Rosenbrock function)
def rosenbrock(Z):
x, y = Z
return (1 - x)**2 + 100 * (y - x**2)**2
def differential_evolution(f, bounds, popsize=20, mutation=0.8, recombination=0.7, maxiter=100):
# Initialize population with random values within the bounds
pop = np.random.rand(popsize, len(bounds))
min_b, max_b = np.asarray(bounds).T
diff = max_b - min_b
pop = min_b + pop * diff
# Evaluate the initial population
fitness = np.asarray([f(ind) for ind in pop])
# Find the index of the best individual
best_idx = np.argmin(fitness)
best = pop[best_idx]
# Evolution loop
for i in range(maxiter):
# Iterate over the population
for j in range(popsize):
# Select three other individuals different from the current one
candidates = [idx for idx in range(popsize) if idx != j]
a, b, c = pop[np.random.choice(candidates, 3, replace=False)]
# Generate a mutant individual using the mutation factor
mutant = np.clip(a + mutation * (b - c), min_b, max_b)
# Generate a trial individual using the recombination factor
cross_points = np.random.rand(len(bounds)) < recombination
if not np.any(cross_points):
cross_points[np.random.randint(0, len(bounds))] = True
trial = np.where(cross_points, mutant, pop[j])
# Evaluate the trial individual
f_trial = f(trial)
# Replace the current individual if the trial is better
if f_trial < fitness[j]:
fitness[j] = f_trial
pop[j] = trial
# Update the best individual if the trial is better
if f_trial < fitness[best_idx]:
best_idx = j
best = trial
yield pop, fitness, best
# Set the bounds for the function to be optimized
bounds = [(-5, 5), (-5, 5)]
fig, ax = plt.subplots()
ax.set_xlim(bounds[0])
ax.set_ylim(bounds[1])
# Create a scatter plot of the initial population
scat = ax.scatter([], [], edgecolors='w', facecolors='C1')
# Create a grid of values
x = np.linspace(bounds[0][0], bounds[0][1], 100)
y = np.linspace(bounds[1][0], bounds[1][1], 100)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])
levels = 10 ** np.linspace(-2, 4, 20)
plt.contour(X, Y, Z, levels=levels, cmap='Greys_r', zorder=-100)
# Define the update function for the animation
def update(frame):
pop, _, _ = frame
scat.set_offsets(pop)
return scat,
# Create the animation
ani = FuncAnimation(fig, update, frames=differential_evolution(rosenbrock, bounds),
blit=True, interval=100, cache_frame_data=False)
# Show the animation
plt.close()
HTML(ani.to_html5_video())
Finally, we have a category of algorithms that can learn from examples. One could see this category as a family of algorithms that update their code (or parameters) based on a learning process.

Fig. 10 Machine learning is only one branch of AI and the learning processes are commonly divided into three categories: supervised, unsupervised, and reinforced learning. Deep learning is a subpart of the machine learning family.#
What is machine learning?
“Field of non-trivial data analysis of complicated data sets”
ML involves
data description, interpretation
prediction
inference, i.e. learning from the data
Algorithms
can extract information from high dimensional data
find general properties, structures of the data
we can map those properties to physical interpretation
What is NOT machine learning?
“A ~magical~ universal analysis of complicated data sets”
ML does not provide
data compilation, and understanding
scientific interpretation
critical thinking
Algorithms
Should never remain a black box
Will always return “an” answer
Why should we care about machine learning?#
We are constantly pushing the boundaries of what can be known and understood. Incomplete or empirical physics is a field that presents us with an ever-changing cutting edge – one that may never truly be fully explored. This makes it both challenging and exciting for scientists to work in this area, as they strive to expand our collective knowledge base.
At the same time, incomplete or empirical physics also brings its own set of challenges when dealing with data collection and analysis. We often find ourselves overwhelmed by noisy, biased and incomplete measurements. These measurements represent highly nonlinear processes, which alone linear relations cannot always describe accurately. To interpret correctly, researchers must first clean up any inconsistencies and account for calibration issues before attempting further analysis into their findings.
Scientists continuously develop new techniques such as machine learning algorithms which allow them to better understand complex datasets by automating certain tasks associated with data cleaning, exploration, modeling, etc. By utilizing such tools in combination with traditional methods (e.g., statistical regression), researchers can gain valuable insights from even seemingly impossible datasets.
By employing sophisticated algorithms and statistical models, machines can discern patterns, detect anomalies, and generate predictions from vast datasets. This data-driven approach empowers scientists to sift through enormous volumes of data. enabling them to uncover hidden relationships, classify objects, and even predict future events.
But why should we, as astronomers, care about machine learning? The answer lies in the vast potential it holds to revolutionize our understanding of the universe. With its ability to handle complex data, machine learning enables scientists to tackle challenges that were previously insurmountable.
Machine learning methods enable us to develop analysis methods that are fast, scalable, and better than anything currently available. We need these methods to be understandable or interpretable so we can explain them and maybe discover new physics without relying on running codes for (accademically) infinite periods of time.
At the same time, however incomplete they may be, these models must still provide accurate predictions and forecasts—otherwise their utility will quickly diminish. That means finding ways to create systems with enough accuracy for us to trust their results while avoiding pitfalls associated with overfitting data or making overly-simplistic assumptions about reality as a whole.
Fortunately there have been some promising advances in this area recently; researchers have developed techniques such as Bayesian networks which allow us make educated guesses about future outcomes based on past observations without having an exhaustive calculation of all possible variables involved in any given situation. Furthermore artificial intelligence (AI) has become increasingly capable at taking raw data from experiments and turning them into actionable insights faster than ever before – allowing scientists more freedom pursue creative solutions.
Overall then it appears that physics is entering a new era where traditional approaches aren’t always sufficient anymore—and creativity combined with technology could help unlock brand-new discoveries beyond our current understanding!
The “Big Data” challenges in astronomy#
The “Big Data” challenges in astronomy are becoming increasingly demanding and complex as the amount of data produced by astronomical observations continues to grow exponentially. Scientists must be able to effectively manage and analyze this vast quantity of information while still maintaining a high level of accuracy and understanding.
This requires an mastering not only of traditional methods such as spectroscopy, but also being knowledgeable about photometry, time series, instruments, surveys, etc, so called multi-messenger information.

Fig. 11 Examples of the data volumes in the GAIA and Rubin surveys.#
In this context, scientist must forget visual inspection of some data. Cutting-edge tools like machine learning algorithms and artificial intelligence techniques provide the automated processing to detect transient events, make forecasting predictions, classification, detect anomalies, and do complex inference. In addition, it is essential for astrophysicists to have an appreciation for the importance that data storage solutions play in managing large datasets efficiently and securely.
Terminology#
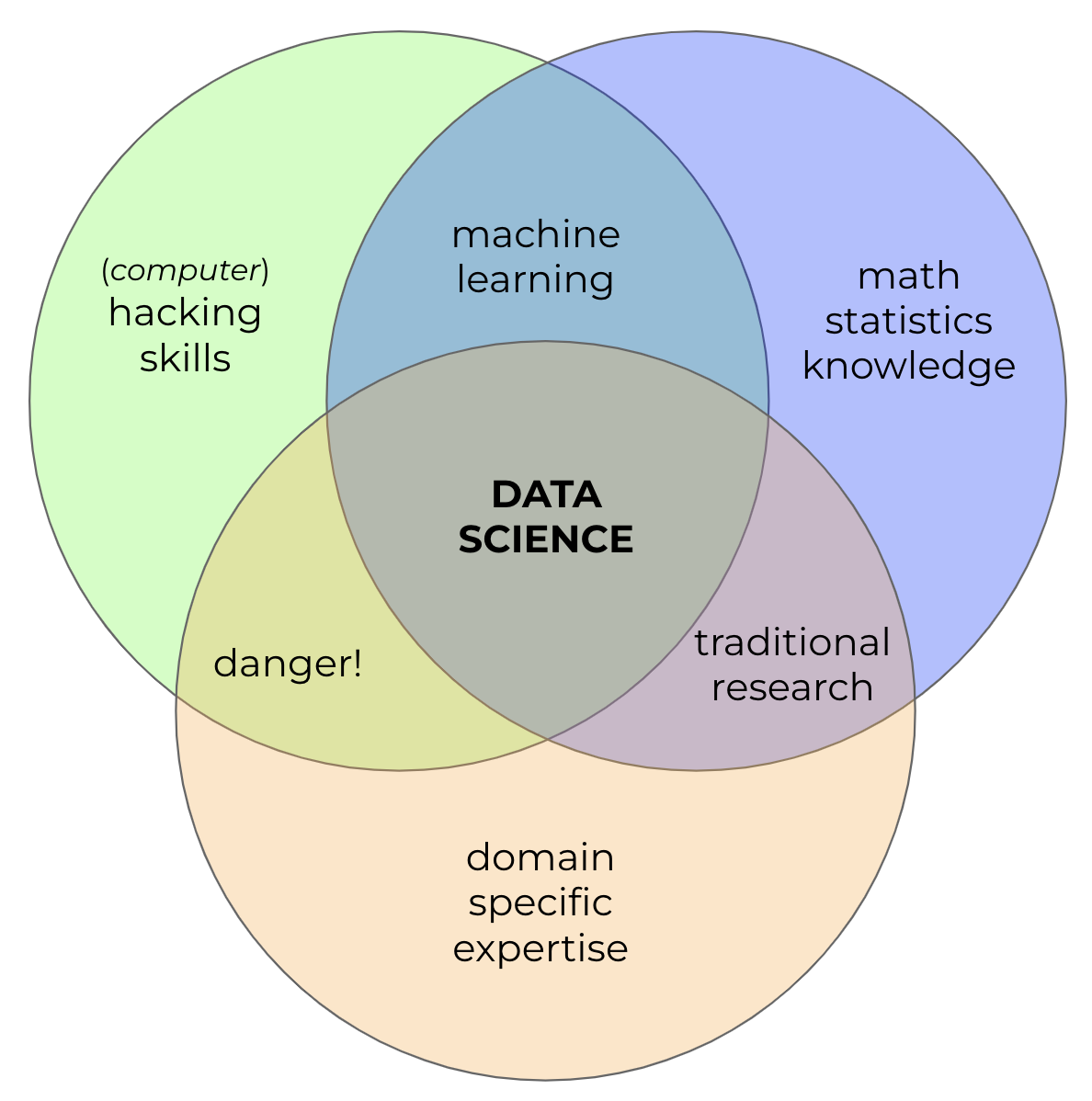
Fig. 12 Data science is the intersection of three important skills: mathematics/statistics, computer science, and specific domain expertise.#
Data science is a rapidly growing field of study that combines the power of mathematics, computer science, and domain expertise to unlock insights from data. Data scientists are experts in extracting knowledge from large amounts of data using a variety of techniques such as machine learning algorithms, statistical analysis, predictive modeling, natural language processing (NLP), visualization tools and more. By leveraging the strengths each discipline brings to the table it allows for powerful solutions that would not otherwise be possible with any one skill alone. For example: predicting disease outbreaks require epidemiological background along with advanced analytics; detecting fraud needs financial acumen combined with sophisticated pattern recognition algorithms. Where traditional research was mostly based on domain expertise and mathematics, data science requires solid computer skills to manipulate and extract knowledge from large amounts of complex data.
Machine learning is the intersection of only computer science and mathematics. The intersection of these two disciplines makes machine learning an incredibly useful tool for many scientific applications. However, this same complexity also means there is potential for misinterpretation or misuse. Without proper understanding of the underlying principles behind how machines learn from data sets, results may be inaccurate or even misleading when applied to realworld scenarios without further investigation into their validity first. In other words, machine learning per se does not have domain expertise and so requires the users to have a minimum understanding and sufficient caution to properly interpret the results.

Fig. 13 Machine learning is the intersection of computer science and mathematics and lacks domain expertise required to properly interpret the outputs.#
Training a model#
In machine learning the training set matters gianormously to make our models accurate and performant.
To understand it better, I always use the elephant parable.
Six blind persons are asked to describe an elephant by touching its body parts. A first one feels its side and describes it as a wall, a second touches its tusk and thinks it is a spear, a third one feels the trunk and confidently identifies a snake, a fourth touches a knee and believes it could be a tree, the fifth palps the ear and thinks of a fan and, finally, a sixth holds the tail and assumes the elephant is a rope.
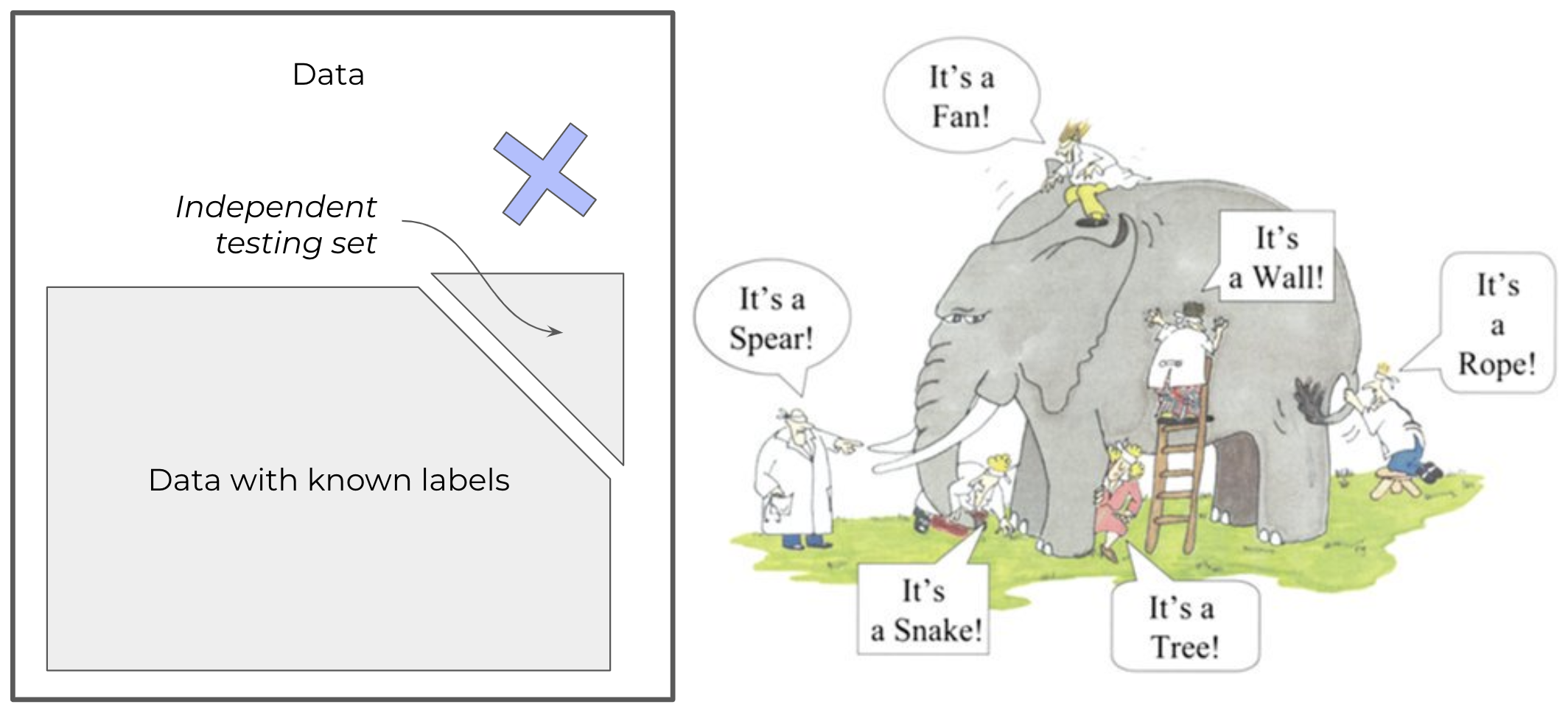
Fig. 14 The elephant parable or how important the training set could be to get the whole picture.#
None of the blind people was wrong in their analysis. They plausibly described what they touched and felt. The challenge comes from their limited perception. They each assumed their interaction was representative of the full picture, but they were wrong.
This parable represents exactly what training sets do to machine learning. But often it could be hard to know it’s an elephant, we don’t always have the whole picture to check.
The training set must be sufficiently representative of the whole picture to lead to the right conclusion. If any of the blind people would cross check with another, their conclusions would most likely be different.
Validating: the “Generalization problem”#
It is critical to understand the importance of validating and testing a machine learning model.
Validation is an essential step when developing a machine learning model as it ensures that the training set accurately represents what will happen during application deployment. To validate a machine learning model, one should mask part of their training set and use this blind test on their trained algorithm or neural network before deploying into production environment . It’s also important for validation sets not only contain representative elements but also unseen elements so as to properly assess how well your system can adapt given new inputs and scenarios which may occur during its applications.
Validating and testing your algorithms with unseen data helps ensure we created an accurate representation of reality and that we identify any potential issues before they become critical errors down the line.
At its core, validatinga ML Model is testing and understanding the limits of our system’s ability at adapting given new input parameters while still maintaining accuracy throughout all possible scenarios within our application domain. This adaptation is a generalization problem
Training, testing, applying: the three inevitable ones
Training: Giving (labeled or unlabeled) data to your method and letting it find a mapping between input and output variables.
Testing: Using a new piece of data to check the mapping works outside the training. Determines performance of the model.
Applying: Applying to a dataset that is neither trained or tested on, for which the “correct” answer is unknown.
Generalizing: Enabling applications to other “domains” (e.g. extrapolating).
